Conditional Displacement Readout

Created: June 4, 2025 3:31 PM

Single-Qubit and Derivation

The dispersive hamiltonian (from https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.122.080503) in the frame rotating at $\omega_r$ is

$$\hat{H}''/\hbar \approx (\Delta + \chi)\hat{\sigma}_{+}\hat{\sigma}_{-} + \left[ \left( \Omega_q + i\Omega_r \frac{\chi}{g} \right) \hat{\sigma}_{+} + \text{H.c.} \right] - \chi\hat{\sigma}_z\hat{a}^{\dagger}\hat{a} + \left[ \left( i\Omega_r - \Omega_q \frac{\chi}{g}\hat{\sigma}_z \right) \hat{a}^{\dagger} + \text{H.c.} \right]$$

Note that the approximations for two-level systems has been made, to make $\chi=\frac{g^2}{\Delta}$

The virtual origin $\alpha_{vo}$ is given by

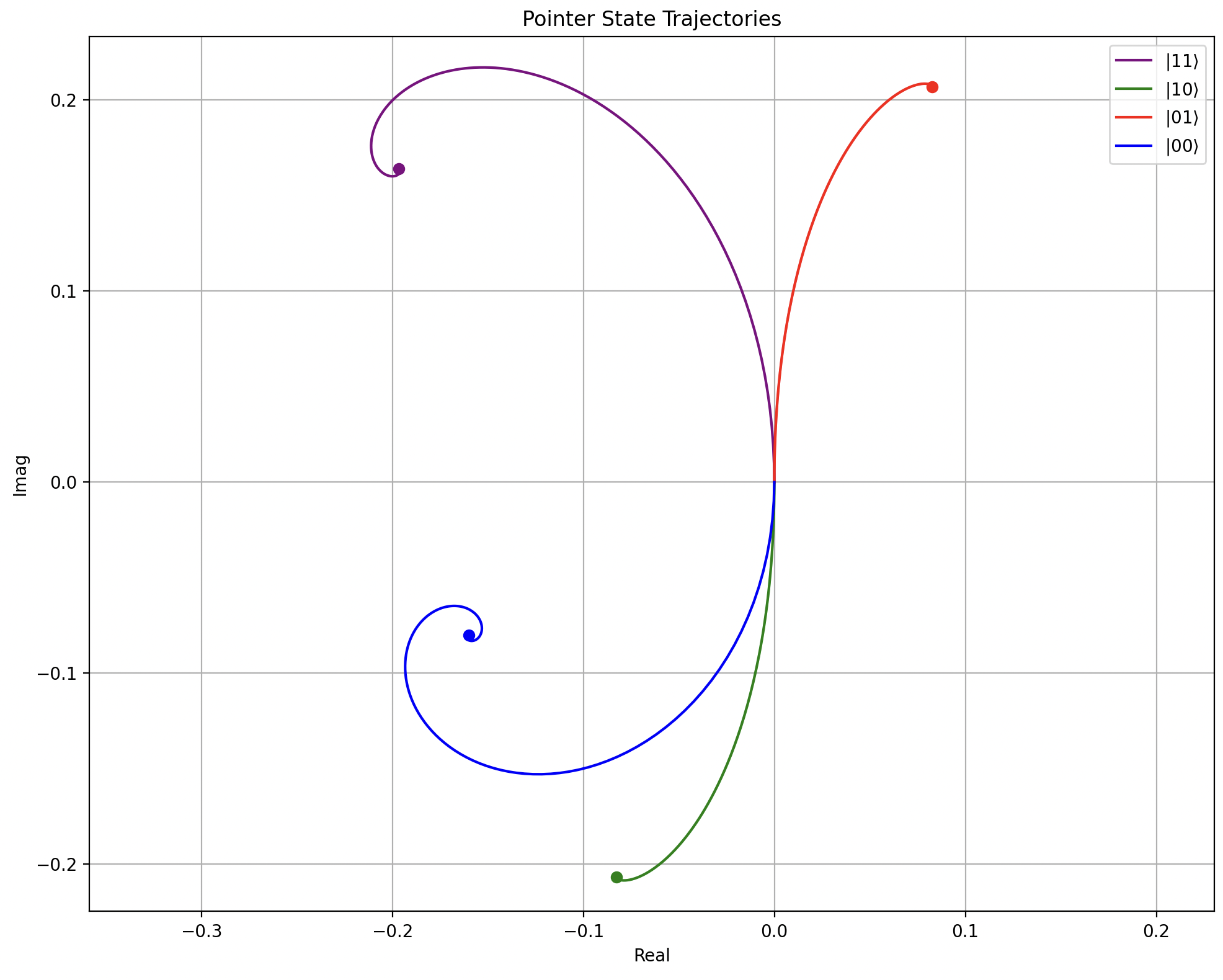
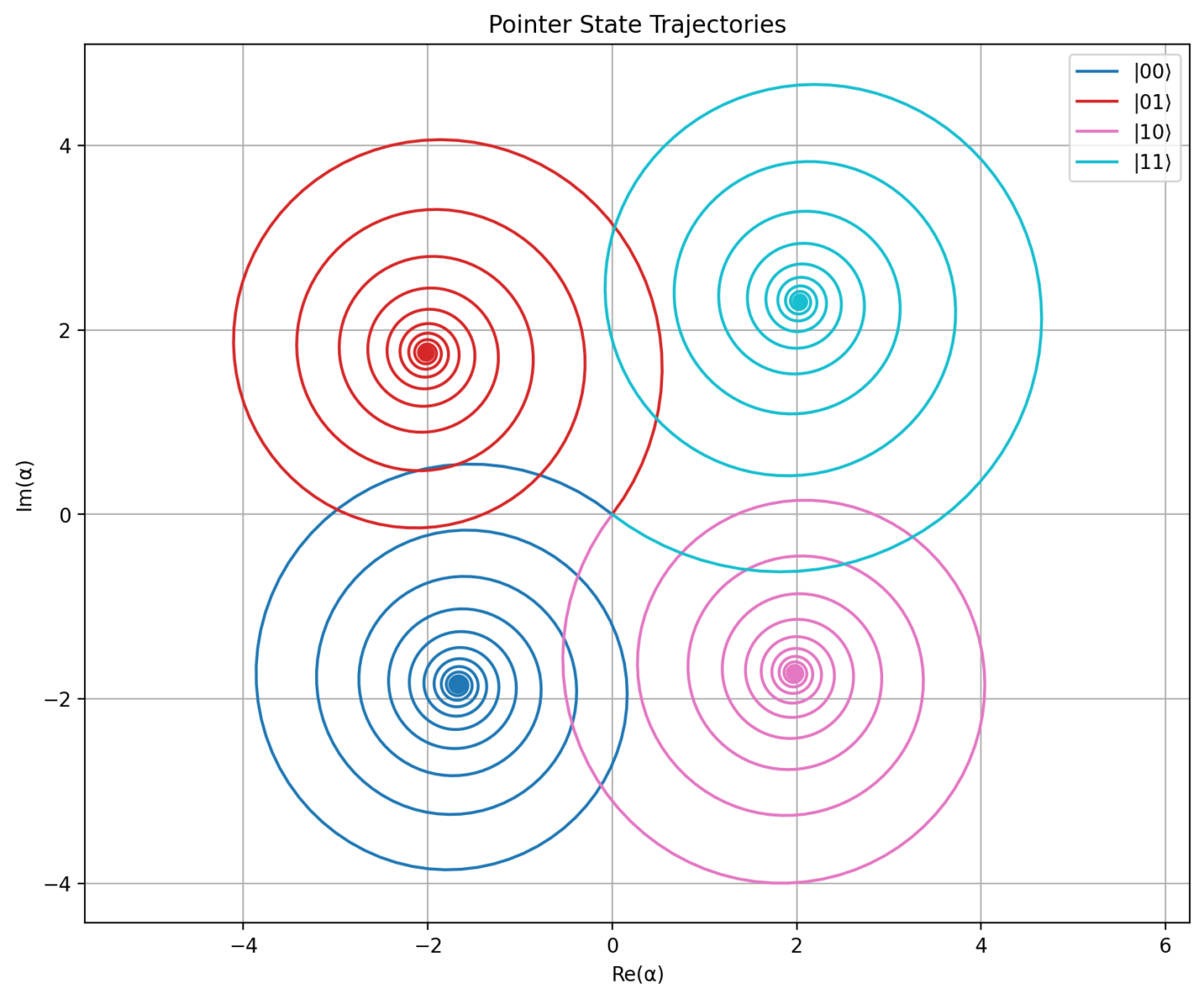
$$\alpha_{vo}=\frac{-\Omega_q}{g}$$

We can visualize this “origin shift” by calculating the pointer state trajectories.

Heisenberg-Langevin Pointer State Trajectories

Using the Heisenberg-Langevin equation

$$\dot{\hat{a}}(t) = -\frac{i}{\hbar}[\hat{a}, \hat{H}''] - \frac{\kappa}{2} \hat{a}(t) + \sqrt{\kappa}\, \hat{a}_{\text{in}}(t)$$

we first calculate the commutators

$$-\frac{i}{\hbar}[\hat{a}, -\hbar \chi \hat{\sigma}_z \hat{a}^\dagger \hat{a}] = i \chi \hat{\sigma}_z \hat{a}\\ -\frac{i}{\hbar} \left[ \hat{a}, \hbar \left( i\Omega_r - \Omega_q \frac{\chi}{g} \hat{\sigma}_z \right) \hat{a}^\dagger + \text{H.c.} \right] = \Omega_r + i \Omega_q \frac{\chi}{g} \hat{\sigma}_z$$ $$\frac{d}{dt} \hat{a}(t) = -\left( i \chi \hat{\sigma}_z + \frac{\kappa}{2} \right) \hat{a}(t) + \left( \Omega_r + i \Omega_q \frac{\chi}{g} \hat{\sigma}_z \right)$$ $$\dot{\alpha}(t) = -\left(i\chi\sigma_z + \frac{\kappa}{2}\right)\alpha(t) + \Omega_r + i\Omega_q\frac{\chi}{g}\sigma_z$$ $$\alpha(t) = \alpha_{ss} + \left(\alpha(0) - \alpha_{ss}\right) e^{-\left(i\chi\sigma_z + \frac{\kappa}{2}\right)t}$$ $$\alpha_{ss} = \frac{i\Omega_r + \Omega_q\frac{\chi}{g}\sigma_z} {\frac{i\kappa}{2} + \chi\sigma_z+\delta_r}$$

Plots

Two coupled qubits case

The two coupled qubit case is described by the hamiltonian

$$\hat{H} = (\Delta_1 + \chi_1) \hat{\sigma}_{+,1} \hat{\sigma}_{-,1} + (\Delta_2 + \chi_2) \hat{\sigma}_{+,2} \hat{\sigma}_{-,2} - \chi_1 \hat{\sigma}_{z,1} \hat{a}^\dagger \hat{a} - \chi_2 \hat{\sigma}_{z,2} \hat{a}^\dagger \hat{a} + \left( \Omega_{q1} + i \frac{\Omega_r \chi_1}{g_1} \right) \hat{\sigma}_{+,1} + \left( \Omega_{q1} - i \frac{\Omega_r \chi_1}{g_1} \right) \hat{\sigma}_{-,1} + \left( \Omega_{q2} + i \frac{\Omega_r \chi_2}{g_2} \right) \hat{\sigma}_{+,2} + \left( \Omega_{q2} - i \frac{\Omega_r \chi_2}{g_2} \right) \hat{\sigma}_{-,2} + \left( i \Omega_r - \frac{\Omega_{q1} \chi_1}{g_1} \right) \hat{\sigma}_{z,1} \hat{a}^\dagger + \left( -i \Omega_r - \frac{\Omega_{q1} \chi_1}{g_1} \right) \hat{\sigma}_{z,1} \hat{a} + \left( i \Omega_r - \frac{\Omega_{q2} \chi_2}{g_2} \right) \hat{\sigma}_{z,2} \hat{a}^\dagger + \left( -i \Omega_r - \frac{\Omega_{q2} \chi_2}{g_2} \right) \hat{\sigma}_{z,2} \hat{a}$$

We also note the effective total drive of the qubit system,

$$\varepsilon_{\text{eff}}(\sigma_{z,1}, \sigma_{z,2}) = \Omega_{r} - i \left( \Omega_{q1}\frac{\chi_1 \sigma_{z,1}}{g_1} + \Omega_{q2}\frac{\chi_2 \sigma_{z,2}}{g_2} \right)$$

which we note is identical to the single-qubit drive with each parameter split. The $\sigma_z$ is projected into $\pm1$ depending on the state of the qubit.

Recalculating the steady-state pointer in IQ-space,

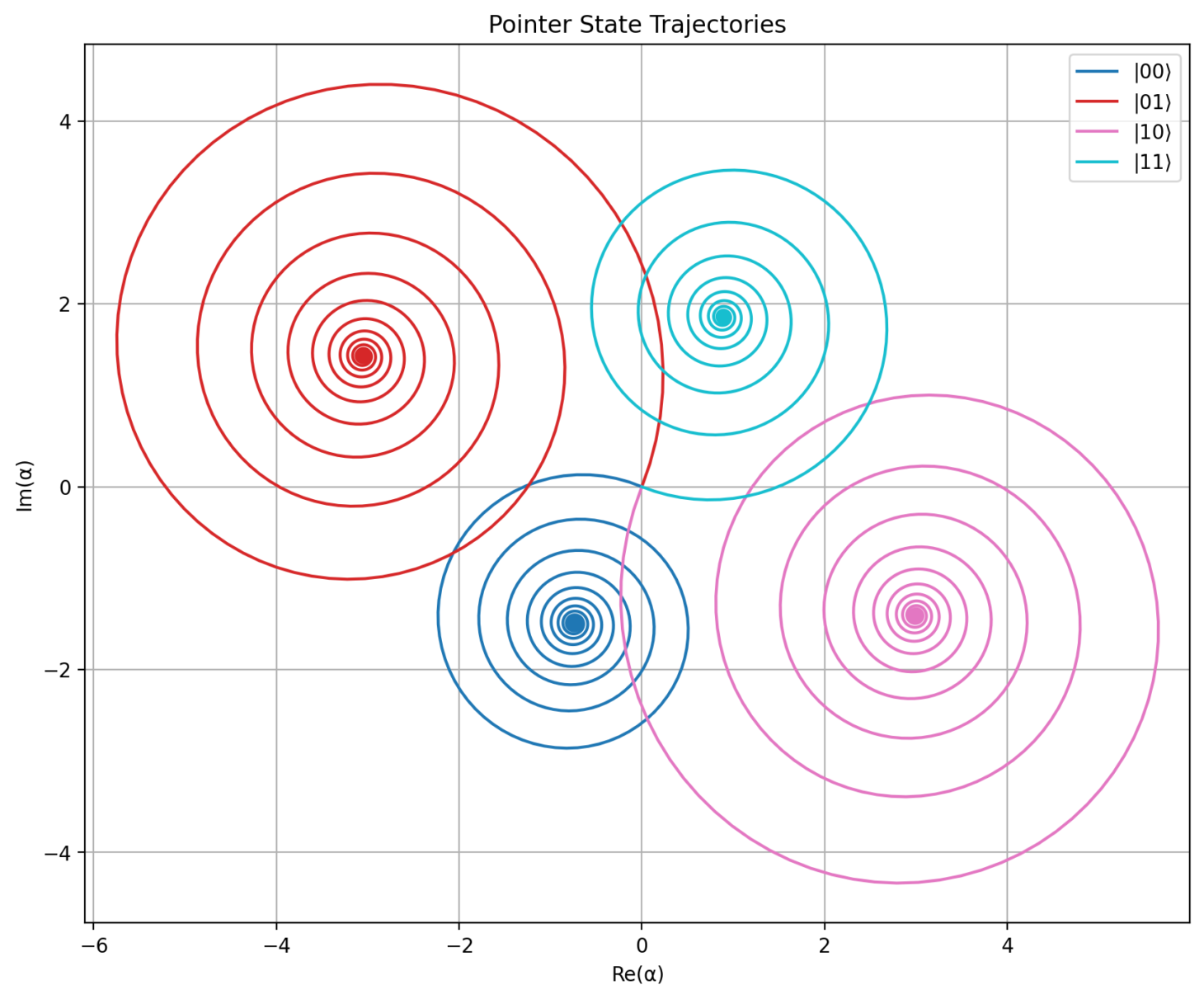
$$\alpha_{ss}=\frac{-\varepsilon}{i\kappa/2+\delta_{r}+\chi_1\sigma_{z,1}+\chi_2\sigma_{z,2}}$$

In our case, we want $\ket{10}$ and $\ket{01}$ to be indistinguishable in this IQ-space. This is first achieved by having $\chi_1=\chi_2$:

in this case, the magnitudes of the drives $\Omega_q$ are equal and simply shifted 180 degrees in phase. However, with unequal $\chi$, the states are no longer on the same point:

no parameters were changed between the two, having the same drives, but $\chi_1$ is now 1/4 of $\chi_2$. To account for this, we find an expression to change the drive pulses

$$\alpha_{10}=\alpha_{01}\\ \frac{-i\Omega_{r} - \left( \Omega_{q1}\frac{\chi_1}{g_1} + \Omega_{q2}\frac{-\chi_2}{g_2} \right)}{i\kappa/2+\delta_{r}+\chi_1-\chi_2} = \frac{-i\Omega_{r} - \left( \Omega_{q1}\frac{-\chi_1}{g_1} + \Omega_{q2}\frac{\chi_2}{g_2} \right)}{i\kappa/2+\delta_{r}-\chi_1+\chi_2}$$

after some cross multiplying, we end with

$$|\Omega_{q1}|=\frac{\chi_1g_2}{\chi_2g_1}|\Omega_{q2}|$$

after re-simulating, we find

(the only parameter changed between this graph and the previous one was $\Omega_{q2}$). Letting $\phi_2=0$, we calculate the phase difference between the two pulses:

$$\phi_1= \tan^{-1}\left( \frac{\chi_2}{g_2} |\Omega_{q2}| + \frac{2\Omega_r (\chi_1 - \chi_2)}{\kappa} \right)- \tan^{-1}\left( \frac{\chi_1}{g_1} |\Omega_{q1}| \right)$$

Multilevel and minimizing SNR

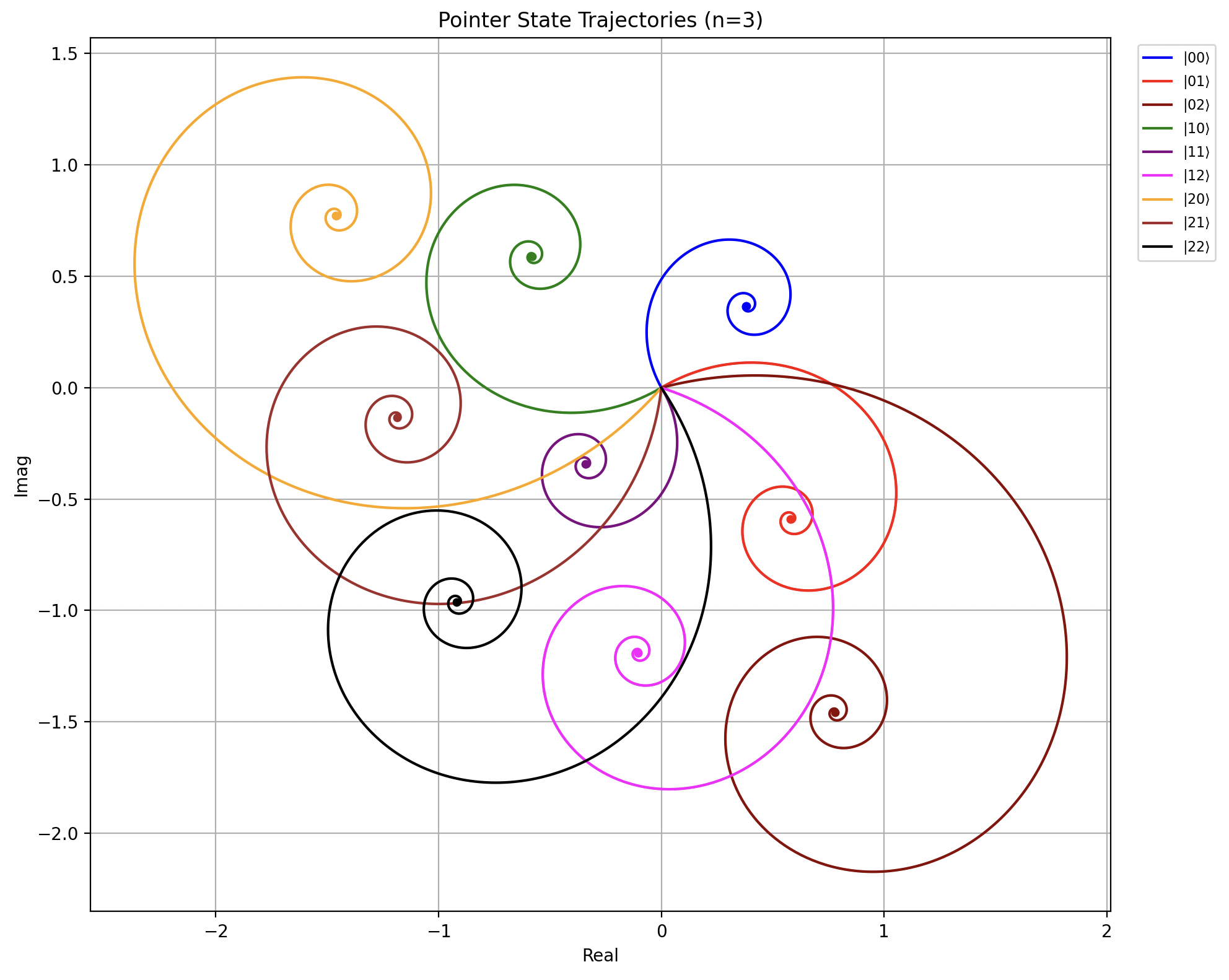
We extend our simulation for multilevel systems, and calculate SNR based on phase-space distance

$$SNR = |\alpha_i - \alpha_j|^2$$

Varying parameters to maximize the minimum SNR between any two states, we find

$\Omega_{q1}=2.000, \Omega_{q2}=1.997, \phi_{q1}=0.000, \phi_{q2}=1.602$

Both $\Omega$ were limited at $2.0$ to speed up iteration - the ratios of magnitude is the significant factor in this case.

Readout Optimization

Optimizing both qubit drives for readout SNR, we consider varying metrics for separating pointer states.

1. Minimum SNR: the minimum SNR between any two states considered.
2. Average SNR: the average SNR between all pairs of states
3. Spacing: ****evenly spacing each pointer state within phase space

With all three considered, we simulate with the following cavity conditions

The plot above is configured for minimum SNR. Below, the left is configured for average, and the right is configured for spacing (visually very similar, but parameters are slightly different).

Measurement-Induced State Transitions - optimization and sim

Measurement Induced State Transitions